Вся информация с других сайтов... и не проверена... Способы определенияГеометрическое определениеОбычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок).
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности. Если α — вещественное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых угловВо многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см.: Теорема синусов, Теорема косинусов). Определение тригонометрических функций как решений дифференциальных уравненийФункции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения с начальными условиями Определение тригонометрических функций как решений функциональных уравненийФункции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через рядыИспользуя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов: Пользуясь этими формулами, а также уравнениями где
Значения тригонометрических функций для некоторых угловЗначения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («N/A» означает, что это значение не определено).
Значения тригонометрических функций нестандартных углов
Свойства тригонометрических функцийПростейшие тождестваПоскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем: Это соотношение называется основным тригонометрическим тождеством. Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее: НепрерывностьСинус и косинус — непрерывные функции. Тангенс и секанс имеют точки разрыва ЧётностьКосинус и секанс — чётные. Остальные четыре функции — нечётные, то есть: ПериодичностьФункции Формулы приведенияФормулами приведения называются формулы следующего вида: Здесь f — любая тригонометрическая функция, g — соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций), n — целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например: Некоторые формулы приведения:
Формулы сложенияЗначения тригонометрических функций суммы и разности двух углов: Аналогичные формулы для суммы трёх углов: Формулы для кратных угловФормулы двойного угла: Формулы тройного угла: Прочие формулы для кратных углов:
Формулы половинного угла: ПроизведенияФормулы для произведений функций двух углов: Аналогичные формулы для произведений синусов и косинусов трёх углов: Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше. Степени
СуммыДля функций от аргумента x существует представление: где угол ϕ находится из соотношений: Однопараметрическое представлениеВсе тригонометрические функции можно выразить через тангенс половинного угла.
Производные и интегралыВсе тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
Тригонометрические функции комплексного аргументаОпределениепозволяет определить тригонометрические функции от комплексных аргументов через экспоненту или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
Комплексные синус и косинус тесно связаны с гиперболическими функциями: Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
|
|
|


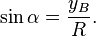
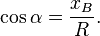







 , то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:


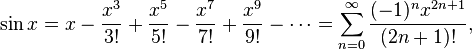


















































































 —
—
 — c периодом
— c периодом











































































































